Logistic Regression

Consider the averge emprical loss function for logistic regression:

J(Θ) = \frac{1}{m} \sum_{i=1}^m log( 1 + e^{(-y^{(i)}Θ^Tx^{(i)})} ) = -\frac{1}{m} \sum_{i=1}^m log( h_Θ(y^{(i)}x^{(i)}) )

where

$y^{(i)} ∈ \{-1,1\}, h_Θ(Θ^Tx)$ and $g(z) = \frac{1}{1 + e^{-z}}$

(a)

Find the Hessian of J(Θ ) and prove it holds true that $Z^THZ ≥ 0$ .

J(Θ) = -\frac{1}{m} \sum_{i=1}^m log( h_Θ(y^{(i)}x^{(i)}) ) = -\frac{1}{m} \sum_{i=1}^m log( sigmoid(y^{(i)}Θ^Tx^{(i)}) )

\frac{\partial J}{\partial Θ_i} = -\frac{1}{m} \sum_{k=1}^m \frac{1}{\partial sigmoid} * \frac{\partial sigmoid}{y^{(i)}Θ^Tx^{(k)}} * \frac{\partial y^{(k)}Θ^Tx^{(k)}}{\partial Θ_i}

= -\frac{1}{m} \sum_{i=1}^m (1-sigmoid(y^{(k)}Θ^Tx^{(k)})) y^{(k)} x^{(k)}_i

J(Θ) is the gradient.

H_{ij} = \frac{\partial J}{\partial Θ_i \partial Θ_j} = -\frac{1}{m} \sum_{k=1}^m -1 * sigmoid (1-sigmoid) * y^{(k)} x^{(k)}_j * y^{(k)} x^{(k)}_i

Since $y^{(i)} ∈ \{-1,1\}, h_Θ(Θ^Tx)$ .

H_{ij} = \frac{\partial J}{\partial Θ_i \partial Θ_j} = \frac{1}{m} \sum_{k=1}^m sigmoid (1-sigmoid) * x^{(k)}_j x^{(k)}_i

$H_{ij}$ is the element of Hessian matrix at row i, col j.

Z^THZ = \sum _{i=1}^n \sum _{j=1}^n Z_i H_{ij} Z_j

= \sum _{i=1}^n \sum _{j=1}^n Z_i Z_j \frac{1}{m} \sum_{k=1}^m sigmoid (1-sigmoid) * x^{(k)}_j x^{(k)}_i

= \frac{1}{m} \sum _{k=1}^n sigmoid(1-sigmoid) * \sum _{i=1}^n \sum _{j=1}^n Z_i Z_j x^{(k)}_j x^{(k)}_i

= \frac{1}{m} \sum _{k=1}^n sigmoid(1-sigmoid) * \sum _{i=1}^n (Z_i x_i^k)^2

$sigmoid ∈ \{0, 1\}, Z^THZ≥0$ , aka, J(Θ) is convex, no local maximum, and Newton method can be applied to J(Θ).

(b) Newton Method Implementation

Now we implement Newton method classification in Python.

Data are provided here:

Import libraries

import numpy as np
import matplotlib.pyplot as plt

Functions for convenience

def theta_x(theta, X):
    return X.dot(theta)

def sigmoid(z):
    return 1./(1. + np.exp(-z))

Now two key functions

Function for gradient

\frac{\partial J}{\partial Θ_i} = -\frac{1}{m} \sum_{i=1}^m (1-sigmoid(y^{(k)}Θ^Tx^{(k)})) y^{(k)} x^{(k)}_i

def gradient_J(theta, X, Y_vector):
    Z = sigmoid(Y_vector * theta_x(theta, X))
    return np.mean((Z-1) * Y_vector * X.T, axis=1)

And function for Hessian

H_{ij} = = \frac{1}{m} \sum_{k=1}^m sigmoid (1-sigmoid) * x^{(k)}_j x^{(k)}_i

def hessian_J(theta, X, Y_vector):
    shape_dim = X.shape[1]
    zs = sigmoid(Y_vector * theta_x(theta, X))

    Hessian = np.zeros([shape_dim, shape_dim])

    for i in range(shape_dim):
        for j in range(shape_dim):
            if i <= j:
                Hessian[i][j] = np.mean(zs * (1-zs) * X[:,j] * X[:,i])
                if i != j:
                    Hessian[j][i] = Hessian[i][j]

    return Hessian

Process data(Poor Python Coding):

X = []
for val in open('x.txt').read().split():
    X.append(float(val))
X = [[x1,x2] for x1,x2 in zip(X[::2],X[1::2])]
X = np.array(X, dtype=np.float128)

Y = []
for val in open('y.txt').read().split():
    Y.append(float(val))
Y = np.array(Y,dtype=np.float128)


red = []
blue = []
for i in range(len(Y)):
    if float(Y[i])==1.:
        red.append(X[i])
    else:
        blue.append(X[i])

red = np.array(red)
blue = np.array(blue)

Plot data

plt.plot(red[:,0],red[:,1],'ro')
plt.plot(blue[:,0],blue[:,1],'bo')

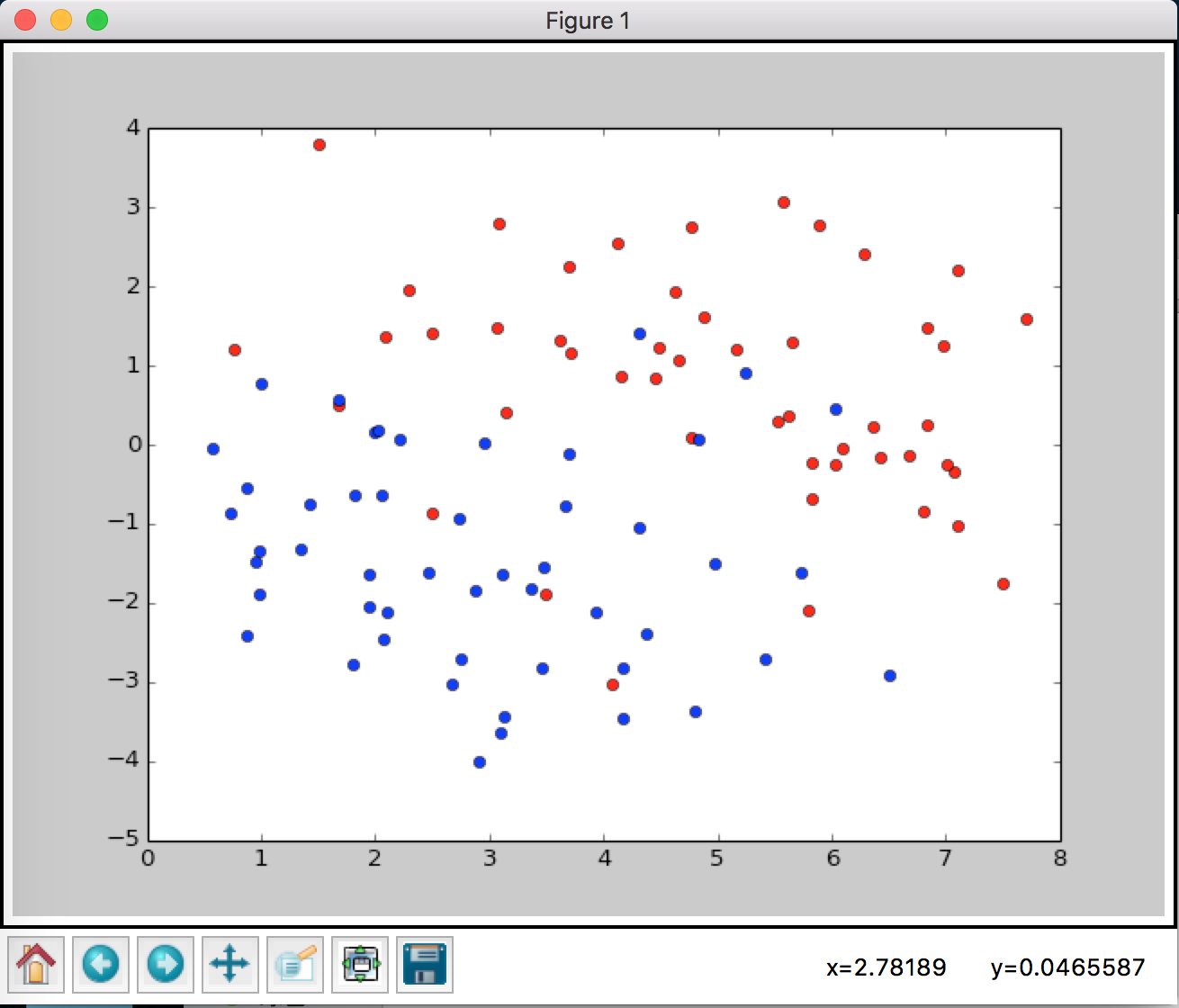
Add pivit and do initialization

X = np.hstack([np.ones([X.shape[0],1]), X])
theta = np.zeros(X.shape[1],dtype=np.float128)
all_thetas = []
error = 1e9

Updata rule for Newton method:

while not converge {

Θ^{t+1} = Θ^t - H^{-1} ∇_ΘJ

}

while error > 1e-7:
    gradient = gradient_J(theta, X, Y)
    Hessian = hessian_J(theta, X, Y)

    delta_theta = np.linalg.inv(Hessian).dot(gradient)
    old_theta = theta.copy()
    theta -= delta_theta
    all_thetas.append(old_theta)
    error = np.sum(np.abs(theta - old_theta))

Plot the learning process:

for __theta in all_thetas:
    print __theta
    
xs = np.array([np.min(X[:,1]), np.max(X[:,1])],dtype=np.float128)

for i, __theta in enumerate(all_thetas):
    ys = (__theta[1] * xs + __theta[0]) / -__theta[2]
    plt.plot(xs, ys, label='Iteration {}'.format(i), lw='0.5')

plt.legend(loc='best')
plt.show()

Output:

[0. 0. 0.]
[-1.50983811  0.43509696  0.62161752]
[-2.21834632  0.64372727  0.95944716]
[-2.55431051  0.74137714  1.13493588]
[-2.61847133  0.75979248  1.1707512 ]
[-2.62050954  0.76037096  1.17194549]
[-2.6205116   0.76037154  1.17194674]

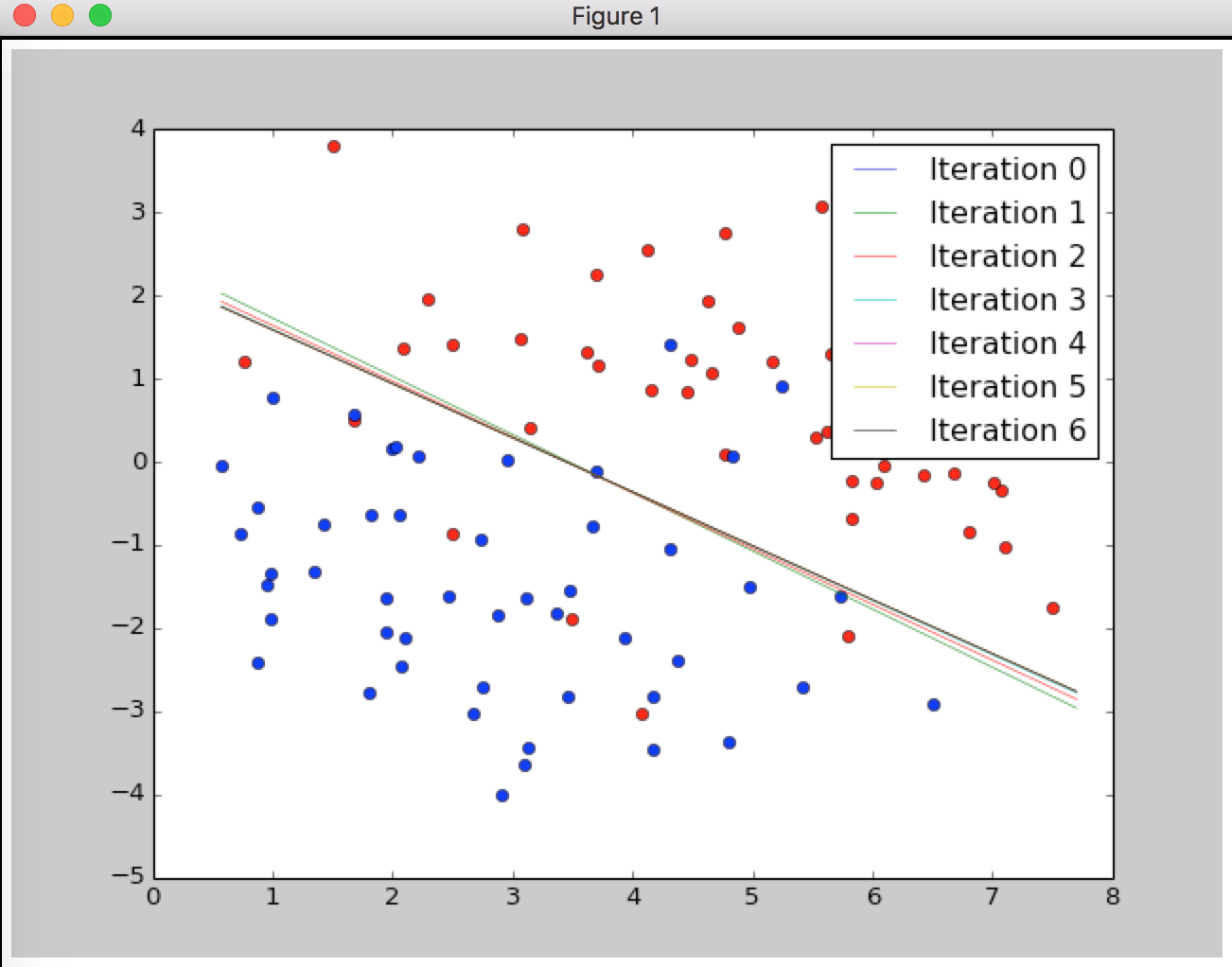
Good!