JR's Machine Learning Notes

K-Nearest-Neighbor Algorithm

Basic Principle

Suppose exists an example set, and each example has a label. Compare every single feature of the new sample with existing sample, and extract the label of the most similiar sample.

Algorithm

Input: Training Set

T = \{(x_1,y_1), (x_2,y_2), ... ,(x_n,y_n)\}

x_i∈X⊆R^n

y_i∈Y = \{ c_1,c_2,...c_k \}

Output: y = class of x

(1) According to given distance measurement, find K nearest points with x in training set, mark the field containing these K points as N_k(x)

(2) In N_k(x), according to classification and decision rule to decide the class of y

Model

The distance between 2 samples is defined as:

L_p(x_i,x_j) = (\sum_{l=1}^n | x_i^l - x_j^l|)^ \frac{1}{p}

(P ≥ 1)

When p=2, Euclidean Distance,

When p=1, Manhattan Distance,

When p= $\infty$ , $L_\infty(x_i,x_j) = max|x^l_i - x^l_j|$ , it's the maximum of the distance in each dimension

Intuition:

Implementation

Now we try to implement this algorithm in Python code :-)

import numpy as np
import operator
import matplotlib.pyplot as plt

create a silly training set

def createDataSet():
    group = np.array([
        [1.0,1.1],
        [1.0,1.0],
        [0.0,0.0],
        [0.0,0.1]
    ])

    labels = ['A','A','B','B']

    return group, labels

Plot the silly dataset

examples, labels = createDataSet()
plt.plot(examples[:,0],examples[:,1],'ro')
plt.xlim([-0.5,1.5])
plt.ylim([-0.5,1.5])
plt.show()

It looks like this

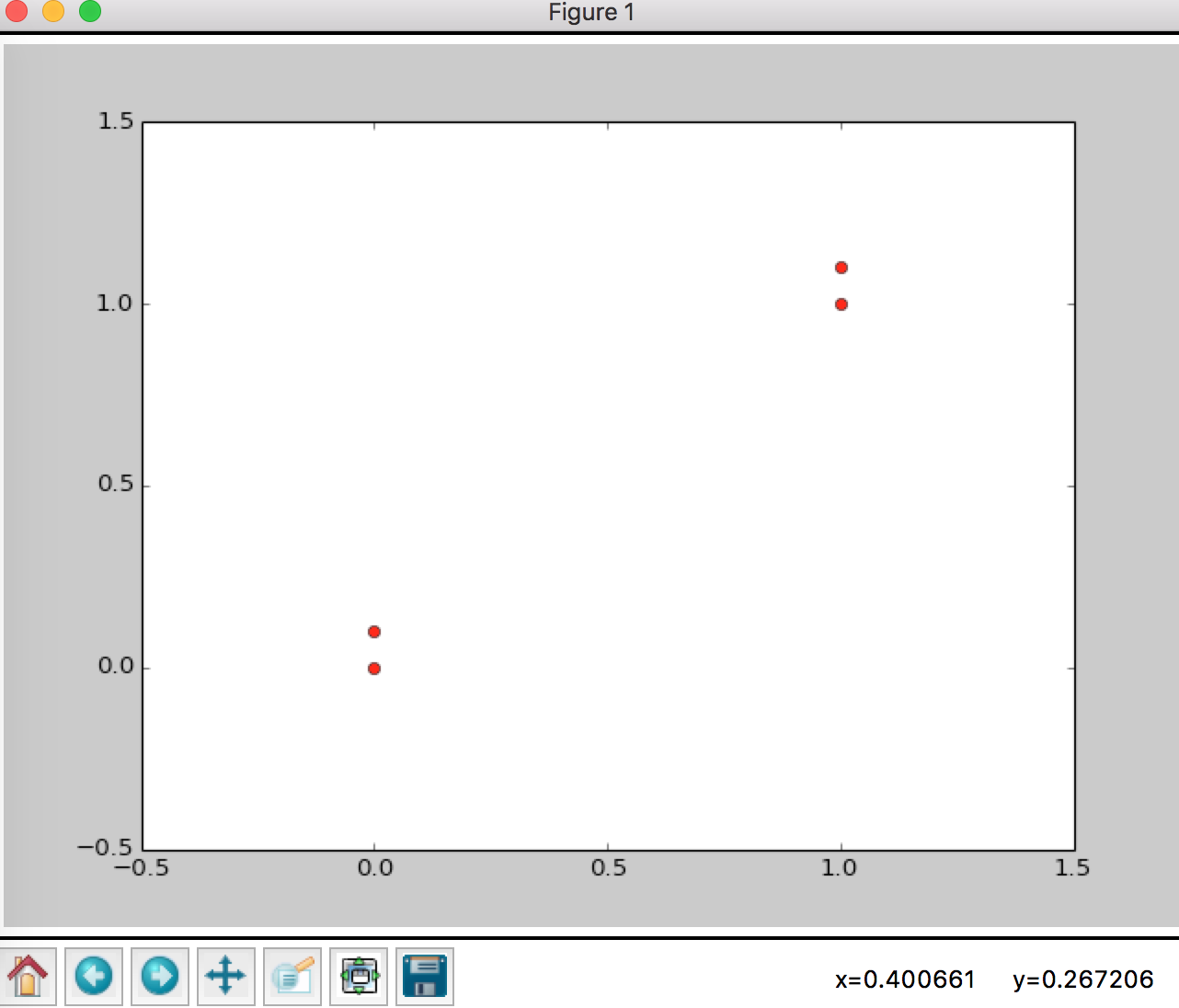
We use Euclidean Distance as distance function Distance between $x^{(1)}$ and $x^{(2)}$

d = ( (x_0^{(1)}-x_0^{(2)})^2 + (x_1^{(1)}-x_2^{(2)})^2 )^\frac{1}{2}

now implement the classify function

def classify(inX, dataset, labels, k):
    # plot the test data (2-dim)
    plt.plot(inX[:,0],inX[:,1], 'bo')
    
    ret = []
    for x in inX:
        dataSize = dataset.shape[0]
        
        # calculate the diff between test data and each traingin data
        diffMat = np.tile(x,(dataSize,1)) - dataset 
        
        diffSquare = diffMat**2;
        disSum     = np.sum(diffSquare,axis=1)
        distances  = np.sqrt(didSum)
        
        # indices of K neighbors
        disIndices = np.argsort(distances)
        
        classCount = {}
        for i in range(k):
            voteLabel = labels[disIndices[i]]
            classCount[voteLabel] = classCount.get(voteLabel, False) + 1
        sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
        
        ret.append(sortedClassCount[0][0])
        
        points = dataset[disIndices[:k],:]
        for point in points:
            relations = np.stack([x,point])
            plt.plot(relations[:,0],relations[:,1], 'green')
    return ret

Let's test our classify function

    examples, labels = createDataSet()
    testData = [
        [0.7,0.7],
        [0.3,0.3]
    ]
    
    // 2-nearest neighbor
    print classify(testData, examples, labels, 2)

output: ['A', 'B']

And the plot look like this

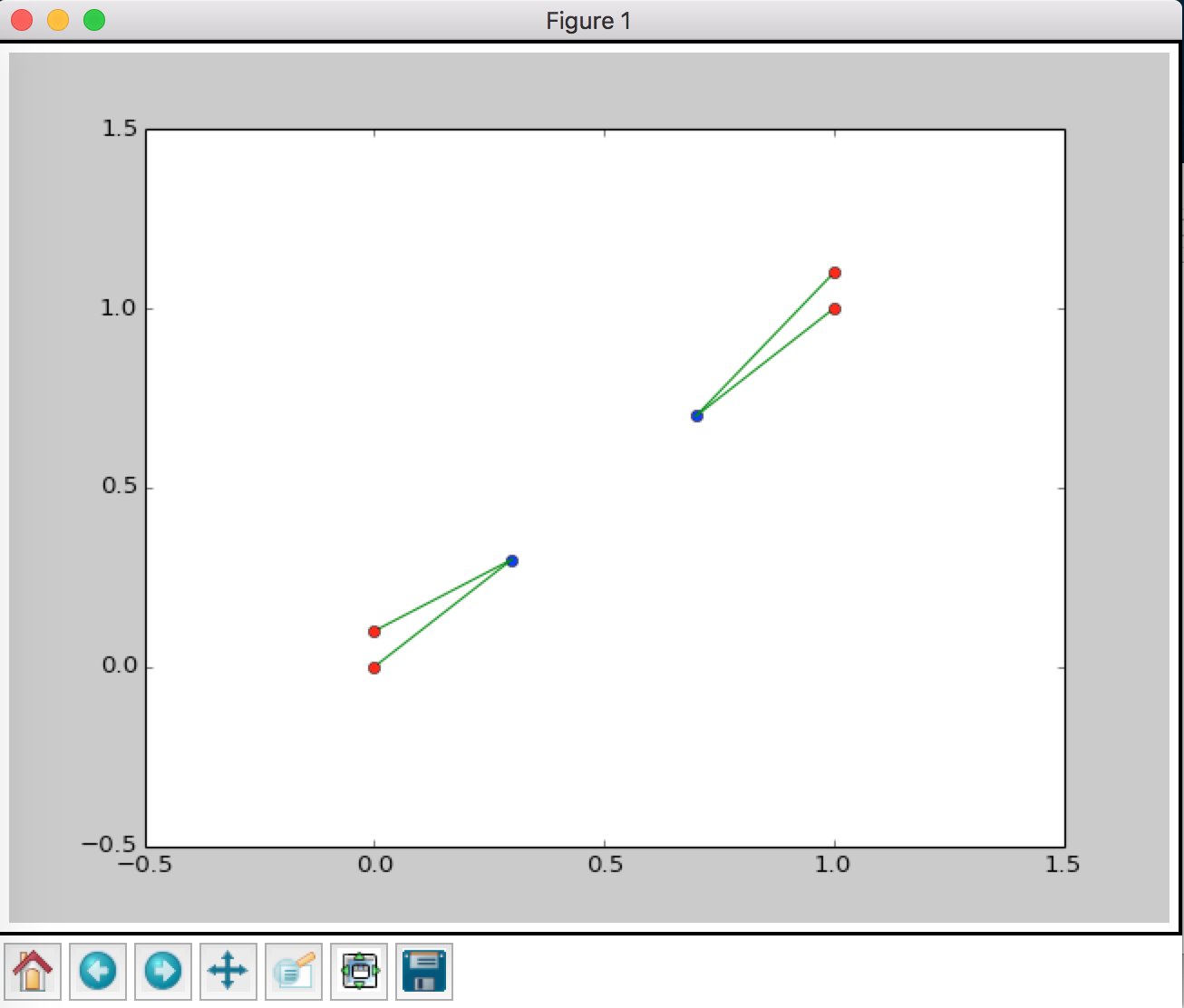
Hummmm, fair enough.