Entropy & Infomation Gain

Entropy

Entropy(熵) indicates the uncertainty of a random variable.

Suppose X is a discrete random variable with finite value, it's probability distribution is

P(X = x_i) = p_i ~~~(i=1,2,..,n)

Then the entropy of X is defined as

H(X) = - \sum^n_{i=1} ~p_i*log(p_i)

From the definition we know that the entropy only relates to X's distribution, not X's value.

Greater uncertainty leads to greater entropy.

Take Bernoulli Distribution as an example. Suppose we have a Bernoulli Distribution pramaterized by p $(0≤p≤1)$ .

P(X=1)=p

P(X=0)=1-p

The entropy of X is

H(X) = -plog_2(p) ~ - ~ (1-p)log_2(1-p)

Looks like

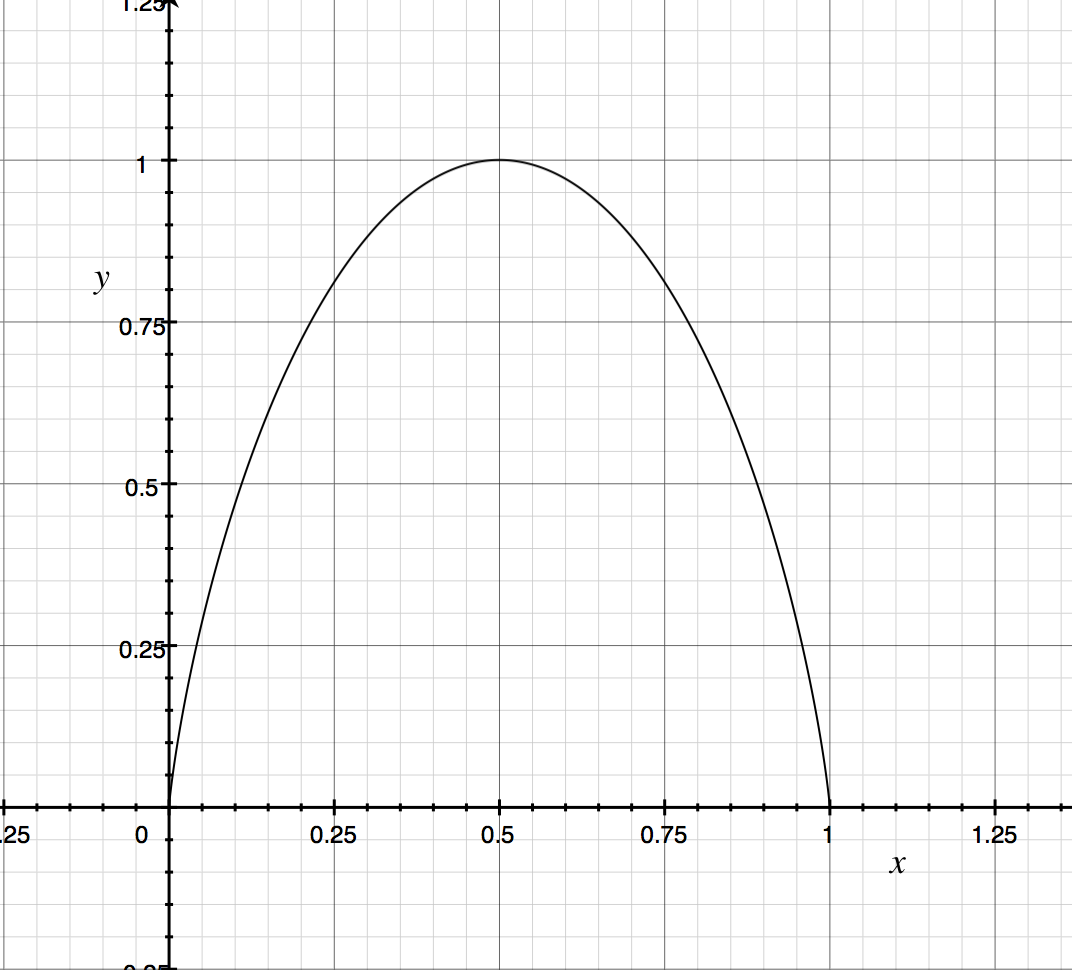
When $p=0$ or $p=1$ , entropy is 0, or say, there's no uncertainty, and when $p=0.5$ , the uncertainty get it's maximum.

Conditional Entropy

Suppose random variable, it's joint probability distribution is

P(X=x_i,Y=y_j) = p_{ij}

i=1,2,...,n~~~;~~~~j=1,2,...,m

Conditional Entropy indicates uncertainty of random variable Y given random variable X, defined as mathematical expectation of $H(Y|X=x_i)$ respect to X

H(Y|X) = \sum^n_{i=1}p_iH(Y|X=x_i)

p_i = P(X=x_i) ~~~ i=1,2,...,n

When probability is get from data approximation(especially Max Likelihood), corresponding entropy and conditional entropyis called empirical entropy and empirical conditional entropy.

Infomation Gain

Infomation Gain indicates how much get infomation of feature $X$ decrease the uncertainty of class $Y$ .

Infomation Gain of feature $A$ to training dataset $D$ is defined as difference of $D$ 's empirical entropy $H(D)$ and empirical conditional entropy given feature $A$

g(D,A) = H(D) - H(D|A)

Intuitively, and literally, information gain is how much knowledge about $D$ we get from giving $A$ .

When build decision tree, we always want to get more information from one single given feature.