Generative Adversarial Network

Intuition

Let's consider the relationship between a money counterfeit criminal and a bank bank clerk.

To be a successful money counterfeit criminal, he keep fake moneys and try to save it into his bank account(let's suppose he won't be caught after failure, what a beautiful society!), and he must fool the bank clerk.

And to keep himself from being fired, the bank clerk must try to identify the counterfeit money.

Everytime the counterfeit money is picked out by the clerk, the criminal go home and invent some new magic to make the counterfeit more delicate. And when the new counterfeit money comes to the clerk, the ability of the clerk is also improved by doing exercise on more delicate counterfeit. Both of them improves their ability in this process.

Professionally, the clerk is our discriminator in GAN and the criminal is the Generator in GAN.

The model roughly looks like this.

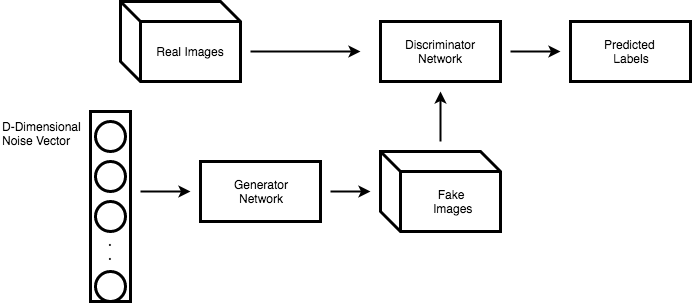
Strategy

Let's call the discriminator and generator $D$ and $G$ respectively,and focus on a specific problem. To generate a one-dollar note from random noise $Z$ . Suppose we have a set of genuine notes $X$ .

The discriminator is actually doing a binary classification, recall the log likelihood function in logistic regression

l(θ) = y^{(i)}log(\hat y^{(i)}) + (1-y^{(i)})log(1-\hat y^{(i)})

In discriminator, $y^{(i)}=1$ indicats the image is real, $y^{(i)}=1$ indicates the image is generated by generator.

x as the input image of discriminator, when $y^{(i)}=1$ , the second term is zero, the first term is

log(D(x))

and when $y^{(i)}=0$ , the first term is 0, and the input image of discriminator is generated by generator, so the second term is

log(1-D(G(Z)))

So the likihood function of the whole GAN is

l(D,G) = log(D(x)) + log(1-D(G(Z)))

And for the discriminator, it tends to do classification right, or say, maximize the likelihood; while the generator tends to fool discriminator, and minimize the likelihood. It turns out to be a $minmax$ problem.

The model of discriminator is

min_{G} max_{D}~l(G,D) = E[logD(x)] + E[1-log(D(G(Z)))]

and the model of generator is

max_{G}~l(G) = E[log(D(G(Z)))]

$x$ is from true data distribution $x$ ~ $p_{data}$ , or $x=G(Z)$ where $Z$ ~ $p_{generator}$ .

Implementation

Now let try to implement a simple GAN with tensorflow, in this simple GAN, we'll try to generate handwritten digit.

First import libraries and training data.

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
import numpy as np
import matplotlib.pyploy as plt

# it's the path to mnist on my computer, you may change it
mnist = input_data.read_data_sets('../../DL_data/MNIST_data')
mnist_images = mnist.train.images
mnist_labels = mnist.train.labels
batch_size = 10

r = 0
def next_batch(data, size):
    global r
    if (r+1)*size > len(data):
        r = 0
        
    ret = data[r*size:(r+1)*size]
    r += 1
    
    return ret

And some functions for convenience.

def initWeight(shape, name):
    val = tf.random_normal(shape=shape, stddev=0.1,dtype=tf.float32)
    return tf.Variable(val, name=name)
    
def initBias(shape, name):
    val = tf.constant(0.2, shape=shape, dtype=tf.float32)
    return tf.Variable(val, name=name)

Now implementation our discriminator. In discriminator, we try to classify real images and fake(generated) images, so it's just like normal image-classification CNN.

The input is a batch of $28*28$ size image with one channel. We do 3 convolutions operations and then there're 2 fully-connected layers, the output is a real number, indicats whether the input is a real image.

class Discriminator():
    def __init__(self):
        # here jut some inits
        with tf.variable_scope('discriminator'):
            self.dW1 = initWeight(shape=[5,5,1,16], name='dW1')
            self.db1 = initBias(shape=[16], name='db1')
            self.dW2 = initWeight(shape=[3,3,16,32], name='dW2')
            self.db2 = initBias(shape=[32], name='db2')

            self.W3 = initWeight(shape=[7*7*32, 128], name='W3')
            self.b3 = initBias(shape=[128], name='b3')
            self.W4 = initWeight(shape=[128,1], name='W4')
            self.b4 = initBias(shape=[1], name='b4')
    
    def forward(self, X):
    self.X = tf.reshape(X, shape=[-1,28,28,1], name='X_reshape')

    conv1 = tf.nn.sigmoid(
        tf.nn.conv2d(self.X, filter=self.dW1, strides=[1,2,2,1], padding='SAME') + self.db1
    )
    # [-1,14,14,16]

    conv2 = tf.nn.sigmoid(
        tf.nn.conv2d(conv1, filter=self.dW2, strides=[1,2,2,1], padding='SAME') + self.db2
    )
    # [-1,7,7,32]
    
    conv2_flatten = tf.reshape(conv2, shape=[-1,7*7*32])

    fc1 = tf.nn.sigmoid(
        tf.matmul(conv2_flatten, self.W3) + self.b3
    )
    '''fc1 = tf.nn.leaky_relu(
        tf.matmul(conv2_flatten, self.W3) + self.b3
    )'''
    #fc1 = tf.matmul(conv2_flatten, self.W3) + self.b3
    # TODO: figure out about activation function

    logits = tf.nn.sigmoid(tf.matmul(fc1, self.W4) + self.b4)
    return logits

Here, we use CNN to extract features of image, since the each single value is the gray scale, it seems reasonable to use $sigmoid$ as the activation function to map values to $[0,1]$ region.

And for fc1, here I've tried $sigmoid$ , $leaky\_relu$ and no activation function, $sigmoid$ performs best, and when there's no activation function, the learning do no proceeding.

And now let implement generator. The generator takes a [1,100] random noise vector as input, perform linear transformation map the noise to [1,784] vector, and reshape it into a single image. Sure it's more reasonable to perform deconv since we're doing with images, but it's just a sample.


class Generator:
    # TODO: Simple linear generation => conv2d_transpose()
    def __init__(self):
        with tf.variable_scope('Generator'):
            self.gW1 = initWeight([100, 256], name='gW1')
            self.gb1 = initBias([256], name='gb1')

            self.gW2 = initWeight([256, 512], name='gW2')
            self.gb2 = initBias([512], name='gb2')

            self.gW3 = initWeight([512, 784], name='gW3')
            self.gb3 = initBias([784], name='gb3')

    def forward(self, z, training=True):
        fc1 = tf.matmul(z, self.gW1) + self.gb1
        #fc1 = tf.layers.batch_normalization(fc1, training=training)
        fc1 = tf.nn.sigmoid(fc1)

        fc2 = tf.matmul(fc1, self.gW2) + self.gb2
        fc2 = tf.nn.sigmoid(fc2)

        fc3 = tf.nn.sigmoid(tf.matmul(fc2, self.gW3) + self.gb3)
        return fc3

And here is the most important part, the loss function. Recall the function

Discriminator:

min_{G} max_{D}~l(G,D) = E[logD(x)] + E[1-log(D(G(Z)))]

Generator:

max_{G}~l(G) = E[log(D(G(Z)))]

d = Discriminator()
g = Generator()

phX = tf.placeholder(dtype=tf.float32, shape=[None, 784])
phZ = tf.placeholder(dtype=tf.float32, shape=[None, 100])

G_out = g.forward(phZ)
D_fake = d.forward(G_out)
D_real = d.forward(phX)

D_loss = -tf.reduce_mean(tf.log(D_real) + tf.log(1.-D_fake))
G_loss = -tf.reduce_mean(tf.log(D_fake))

D_var = [var for var in tf.trainable_variables() if 'Discriminator' in var.name]
G_var = [var for var in tf.trainable_variables() if 'Generator' in var.name]

D_train = tf.train.GradientDescentOptimizer(0.2).minimize(D_loss, var_list=D_var)
G_train = tf.train.GradientDescentOptimizer(0.2).minimize(G_loss, var_list=G_var)

We cannot add D_loss and G_loss and do the minimization together. Because there is $max_G$ and $min_G$ in the formula, we tends to improve the discriminator's ability to identify fake image, but we may end up with making the generator weaker.

Raw codes and numbers are boring, so we may want visualize the images we generate.

Generated_image = tf.reshape(G_out, shape=[28,28])

And finally, we can do the training


with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    MNIST_Digit = mnist_images[mnist_labels==7]

    for i in range(50):
        data_train = next_batch(MNIST_Digit, batch_size)
        for j in range(10):
            sess.run([D_train, G_train], feed_dict={phX:data_train, phZ:np.random.rand(batch_size, 100)})
        image = sess.run(Generated_image, feed_dict={phZ:np.random.randn(1,100)})

        plt.imshow(image, cmap='gray', vmin=0.0, vmax=1.0)
        plt.savefig('generated_images_Seven/generated_{}.png'.format(i))

We try to generate the digital $7$ , why $7$ ? Because I like clearlove.

The result is like

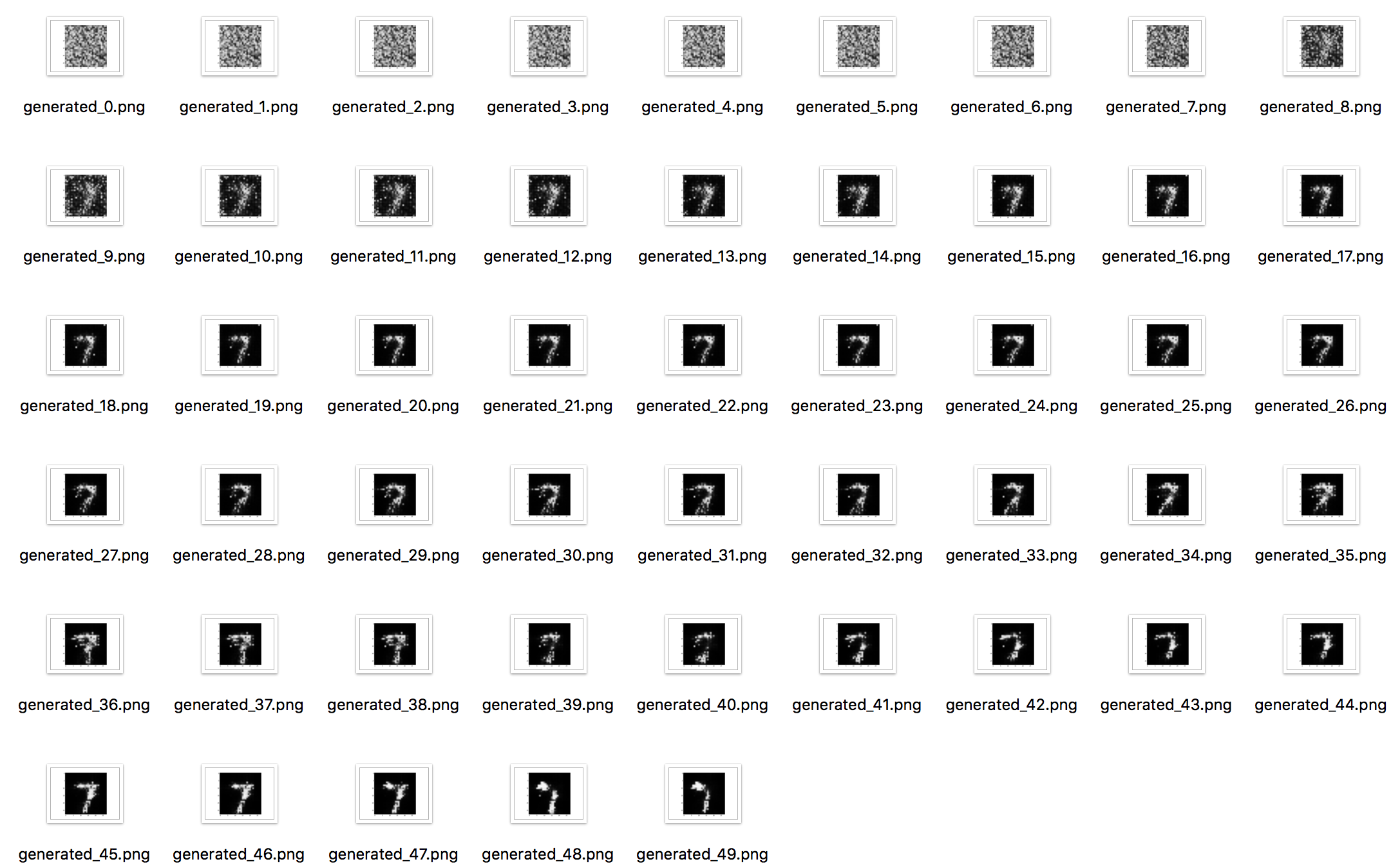
We can see that in first several iteraions, it's just random noise, and $7$ starts to appear gradually.

The whole program is provided here.

Another loss

Here's another kind of loss function that is more straight forward.

We have real images, and generated images. When we train discriminator with real images, we try to make the output of discriminator approch to $1$ s; and When we train discriminator with fake images, we try to make the output of discriminator approch to $0$ s.

Here we use cross entropy to indicates how much the output of discriminator differs with $0$ s and $1$ s.

First, we need a cost function

def cost(logits, labels):
    return tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))

Since we use sigmoid_cross_entropy, we must remove the sigmoid in at the output of discriminator.

And here's the loss function

d = Discriminator()
g = Generator()

phX = tf.placeholder(dtype=tf.float32, shape=[None, 784])
phZ = tf.placeholder(dtype=tf.float32, shape=[None, 100])

G_out = g.forward(phZ)
D_out_real = d.forward(phX)
D_out_fake = d.forward(G_out)

D_real_loss = cost(D_out_real, tf.ones_like(D_out_real))
D_fake_loss = cost(D_out_fake, tf.zeros_like(D_out_fake))


D_loss = D_real_loss + D_fake_loss
G_loss = cost(D_out_fake, tf.ones_like(D_out_fake))


D_vars = [var for var in tf.trainable_variables() if 'Discriminator' in var.name]
G_vars = [var for var in tf.trainable_variables() if 'Generator'     in var.name]

D_train = tf.train.GradientDescentOptimizer(0.05).minimize(D_loss, var_list=D_vars)
G_train = tf.train.GradientDescentOptimizer(0.05).minimize(G_loss, var_list=G_vars)

And the whole program is provided here